How to use a sample size calculator
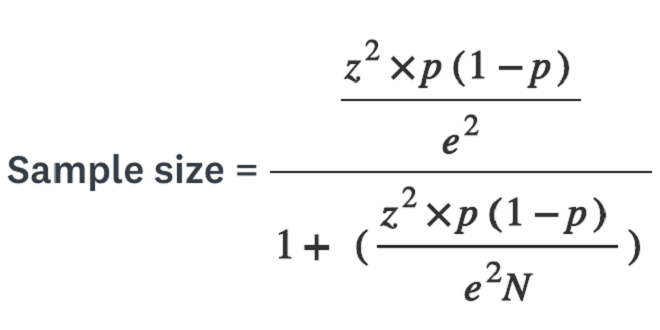
There are many ways you can use a sample calculator. First, you need to determine the distribution of responses. Statistics show that 9 out 10 people will answer yes or no to a question. You can then multiply the proportion of respondents by the number in the sample. This is known as the power or a sample. You will need to have a greater level of confidence if you require a larger sample.
Population size
It is possible to calculate the population size using the entire population sample. This is usually done by using the sample size formula or the z-score. The z-score, which is a numerical representation for the confidence level you want, is usually between 90% to 95%. The formula for the raw score is the average of the population mean and standard deviation divided by the sample size.
The total population must be represented by the sample size. The total population is not represented by the number of non-workers. Consider running a census to confirm the population size if your sample is too small. For a reference, look for studies similar to yours.
Confidence level
A sample size calculator can be used to calculate the number of required samples needed to achieve the desired results. Based on the sample size, the calculator can calculate a margin for error and confidence level. These numbers will assist you in planning your study. They can be confusing. To get the best results, make sure you use the calculator correctly.
First, remember that the greater the sample size, both in terms of error margin and confidence, the lower the confidence level. It is essential to properly use a sample size calculator in your research so that you can make the most of your results and incorporate them into your marketing strategies. How do you select the right size sample?
To determine the right number of samples to use in your research, you can use a sample calculator. This calculator will give you the recommended sample size, margin of error and confidence level. These numbers can be used to help you create the perfect study. How do you use the sample-size calculator? Before you can begin, you will need to be familiar with some factors.
First, you need to know what the standard deviation is. This is the deviation of a data set from its average. This is an approximate estimate of the standard deviation of the population. It’s useful for estimating response variability in a study. The higher the standard deviation, the lower the confidence level. To avoid oversampling, keep your sample size to less than five percent.
Oversampling
A sample size calculator is a great tool for research. It allows you to determine the optimal number of participants and makes it easy to make decisions. Oversampling can result in lower response rates and fatigue which can negatively impact research results. This process is made easy by sample size calculators. Let’s first look at how to calculate sample size. You must first understand the complexity of your problem. Is the population too small? You might need to look at oversampling methods that increase minority population size. While most of the research on oversampling focused on how to avoid noise and where to add samples, very few studies have examined how much sampling is needed.
Margin error
A sample size calculator calculates how many people are required to complete a survey. It does not give the number of samples. A sample must include at least one person to achieve the desired sample size. Research projects generally require a sample size of 250 to 5000 people. The sample proportion p is the percentage of the sample which exhibits the desired characteristic. Once you have determined the sample proportion, multiply it by 100 to get the margin of error.
Last thought
It would be a good idea to calculate the margin of error. This is the chance that a sample average value will be lower or equal than the population mean. If you’re testing the average population value, you should allow for a margin error of no more than ninety-five per cent (95%) After you have determined the sample size, you will be able to calculate the margin of error with a sample size calculator.





